Salah satu cabang matematika adalah trigonometri, yang berkaitan dengan sudut segitiga dan fungsi trigonometri seperti sin, cos, dan tan. Sementara turunan adalah laju perubahan suatu fungsi terhadap perubahan peubahnya. Untuk situasi di mana tingkat perubahan fungsi terletak pada titik a, turunan f(x) ditulis sebagai f'(a). Oleh karena itu, turunan trigonometri adalah proses matematis untuk mendapatkan turunan dari sebuah fungsi trigonometri. Sementara itu, suatu fungsi baru dapat disebut f' (dibaca dengan aksen f). Sin x, cos x, dan tan x adalah fungsi trigonometri umum.
Semua fungsi trigonometri memiliki karakteristiknya sendiri. Perbedaannya tergantung pada jenis bangun segitiga dan besar sudut masing-masing. Sebelum Anda dapat memahami turunannya, Anda harus terlebih dahulu memahami setidaknya tiga fungsi trigonometri yang sering muncul. Ini adalah penjelasannya:
1. sinus (Sin)
Ketika sudut segitiga siku-siku atau salah satu sudutnya 90 derajat, fungsi trigonometri sinus digunakan untuk membandingkan sisi depan segitiga dengan sisi miringnya. Di kuadrannya, fungsi sinus memiliki nilai yang positif dan negatif. Kuadran I dan II menunjukkan sinus positif, sementara kuadran III dan IV menunjukkan sinus negatif.
Fungsi trigonometri cosinus ini adalah perbandingan sisi segitiga yang terletak di sudut dengan sisi miring. Perbandingan ini digunakan dengan catatan segitiga itu adalah segitiga siku-siku atau salah satu sudutnya sebesar 90 derajat. Fungsi cosinus turut memiliki nilai negatif dan positif. Nilai positifnya berada di kuadran I dan IV, sementara nilai negatifnya ada di kuadran II dan III.
3. Tangen (Tan)
3. Tangen (Tan)
Fungsi trigonometri tangen ini berupa perbandingan sisi segitiga yang terletak di depan sudut, dengan sisi segitiga di bagian sudut segitiga tersebut. Perbandingan ini digunakan jika segitiga berupa siku-siku atau salah satu sudutnya sebesar 90 derajat. Fungsi ini memiliki nilai negatif dan positif seperti fungsi trigonometri lainnya. Nilai positifnya berada di kuadran I dan III, nilai negatifnya ada di kuadran II dan IV.
Rumus Turunan Fungsi Trigonometri
Adapun rumus turunan fungsi trigonometri yang memuat fungsi trigonometri berupa sin, cos, tan, cot, sec, dan csc. Berikut ini rumus-rumus tersebut:
1. Jika f (x) = sin x, maka artinya f '(x) = cos x
2. Jika f (x) = cos x, maka artinya f '(x) = −sin x
3. Jika f (x) = tan x, maka artinya f '(x) = sec2 x
4. Jika f (x) = cot x, maka artinya f '(x) = −csc2x
5. Jika f (x) = sec x, maka artinya f '(x) = sec x . tan x
6. Jika f (x) = csc x, maka artinya f '(x) = −csc x . cot x
1. Tentukan y’ dari y = -2 cos x
Jawaban:
y = -2 cos x
y’ = -2 (-sin x)
sehingga, y’ = 2 sin x2. Tentukan hasil dari f (x) = sin (2x + 10)
Jawaban:
f(x) = sin (2x + 10)
f’(x) = 2 cos (2x + 10)
sehingga, y' = 2 cos (2x + 10)
3. Tentukan y’ dari y = 4 sin x + 5 cos x
Jawaban:
y = 4 sin x + 5 cos x
y’ = 4 (cos x) + 5 (-sin x)
sehingga, y’ = 4 cos x – 5 sin x
Turunan Fungsi Eksponensial
Turunan Fungsi Eksponensial
Sebelum membahas lebih jauh tentang turunan fungsi eksponensial, Anda harus mempelajari materi prasyaratnya terlebih dahulu. Turunan fungsi eksponensial agak berbeda dari turunan fungsi aljabar dan turunan fungsi trigonometri.
Mencari bilangan e untuk penurunan fungsi eksponensial
Nilai bilangan real positif e = 2,718281828459, dan rumusnya adalah:
Rumus-rumus turunan fungsi eksponensial
Contoh soal:
Tentukan turunan dari fungsi-fungsi dibawah ini!
(1). Tentukan turunan dari :

[penyelesaian]




2). Tentukan turunan dari :

[penyelesaian]
Turunan Fungsi Logaritma
Fungsi yang merupakan kebalikan dari fungsi eksponensial disebut fungsi logaritma. Direpresentasikan sebagai log b x, dimana b adalah alas log. Nilai x adalah nilai yang sama dengan basis logaritma yang dipangkatkan ke bilangan tetap y, sehingga bentuk umum fungsi logaritma adalah:
y = log bx
Di mana,
- y adalah logaritma dari x,
- b adalah basis logaritma, dan
- x adalah input logaritma.
Beberapa properti fungsi logaritma tercantum di bawah ini:
- log (XY) = log X + log Y
- log (X / Y) = log X – log Y
- catatan X Y = Y catatan X
- log Y X = ln X / ln Y
Rumus turunan fungsi logaritma yang tersedia adalah sebagai berikut.
Turunan dari ln x, log an x, dan ln f(x)
Mari kita bahas rumus ini.
Turunan ln x: Turunan ln x bernilai kebalikan dari x, dengan rumus berikut: (d / dx) dalam x = 1 / x, di mana x lebih besar dari 0.
Turunan log an x: Turunan log dengan basis a dan nilai x bernilai kebalikan dari hasil kali x dan ln a. Rumus turunan log an x adalah: (d/dx) log an x = 1 / [x ln a] Dimana, a ≠ 1.
Turunan ln f(x) : Turunan ln f(x) dapat dihitung sebagai turunan dari f(x) dibagi f(x). Rumus turunan ln f(x) adalah: (d/dx) dalam f(x) = f'(x) / f(x), di mana f(x) adalah sembarang fungsi dari x, dan f'(x) adalah turunan dari fungsi x.
Contoh soal:
(i) Turunan dari log 2x
(ii) Turunan dari log 10 x
(iii) Turunan dari log y
jawaban:
(ii) Turunan dari log 10 x
(iii) Turunan dari log y
jawaban:
(i) Turunan dari log2x
⇒ (d / dx) [log 2x] = (d / dx) [log 2x](d / dx) [2x]
⇒ (d / dx) [log 2x] = 2 / (2x)
⇒ (d/dx) [log 2x] = 1/x
(ii) Turunan dari log 10 x
⇒ (d / dx) [log 10 x] = 1 / [x ln 10]
(iii) Turunan dari log y
⇒ (d / dx) [log y] = [1 / y](dy / dx)

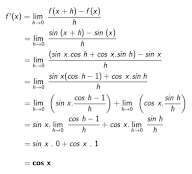












Tidak ada komentar:
Posting Komentar