Turunan Invers Fungsi
Dalam kalkulus, istilah "turunan invers fungsi" mengacu pada penghitungan turunan dari fungsi invers. Jika suatu fungsi f didefinisikan pada suatu interval dan memiliki fungsi invers f-1, turunan invers fungsi diwakili dengan f′-1 (x) atau (f-1)′(x).Oleh karena itu, jika fungsi f(x) adalah fungsi satu-satu kontinu atau fungsi bijektif yang didefinisikan pada suatu interval, katakanlah I, maka fungsi f(x) juga kontinu, dan jika fungsi f(x) adalah fungsi terdiferensiasi, maka fungsi f(x) juga terdiferensiasi.
Rumus untuk Turunan Invers Fungsi adalah sebagai berikut:
Menurut rumus ini, untuk menghitung turunan invers suatu fungsi pada nilai tertentu, kita perlu mengetahui turunan fungsi awal pada nilai invers tersebut.
Ini adalah prosedur umum untuk menghitung turunan invers fungsi:
a. Mengidentifikasi Fungsi Asli:
Misal, y = f(x) dan g(x) adalah fungsi f(x) yang berlawanan.
b. Perhitungan Turunan Fungsi Asli:
Cari turunan f'(x)
c. Untuk mengetahui nilai invers:
Cari nilai invers f-1(x) yang sesuai.
d. Hitung hasil invers:
Untuk menghitung (f-1)′(x), gunakan rumus sesuai langkah sebelumnya, alih-alih menggunakan f-1 (x) dan f'(f-1 (x).
Dalam situasi di mana kita memiliki informasi tentang perubahan suatu variabel terhadap variabel lainnya dan ingin mengetahui perubahan yang terkait dengan inversnya, penurunan invers fungsi sering digunakan.
Contoh soal:
cari turunan invers f(x) = 2x + 3.
Penyelesaian:
Misal f(x) = 2x + 3 dan g(x) adalah invers f(x), yaitu f-1(x). Untuk menghitung turunan invers g'(x), kita perlu mengetahui bahwa f'(x) = 2. Kemudian kita menggunakan rumus ini.
g'(x) = 1/f'(g(x)) = 1/2
Oleh karena itu, turunan fungsi g(x) terhadap x adalah 1/2.
Turunan Invers Trigonometri
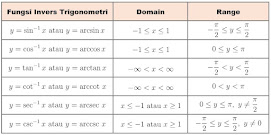
Fungsi invers trigonometri menyebabkan penurunan trigonometri. Dalam trigonometri invers, kita memiliki enam fungsi yang merupakan kebalikan dari enam fungsi trigonometri dasar. Turunan trigonometri invers hanya dapat digambarkan dalam domain fungsi trigonometri invers, yang dapat dilihat sebagai berikut:
Turunan dari fungsi trigonometri invers adalah turunan dari fungsi trigonometri invers, seperti arcsin (atau sin-1), arccos (atau cos-1), dan arctan (atau tan-1), dll. Kami menemukan turunan dari fungsi trigonometri invers dengan menggunakan diferensiasi implisit, yang akan kami bahas secara rinci di bagian mendatang. Turunan invers trigonometri adalah sebagai berikut:
1. Tingkat penurunan arcsin x adalah d/dx(arcsin x) = 1/√1-x2, karena -1 < x < 1.
2. Jika -1 < x < 1, turunan arccos x adalah d/dx(arccos x) = -1/√1-x2.
3. Untuk semua x di R, turunan arctan x adalah d/dx(arctan x) = 1/(1+x2).
4. Ketika x < -1 atau x > 1, penurunan arccsc x adalah d/dx(arccsc x) = -1/(|x|√x2-1).
5. Ketika x < -1 atau x > 1, turunan arcsec x adalah d/dx(arcsec x) = 1/(|x|√x2-1).
6. Untuk semua x di R, turunan arccot x adalah d/dx(arccot x) = -1/(1+x2).
Turunan Invers Logaritma
Dengan mengikuti aturan dasar kalkulus, turunan dari fungsi invers logaritma natural (ln)—juga dikenal sebagai fungsi logaritma natural invers atau ln-1 (x), dan biasanya disebut sebagai exp(x) atau ex—melibatkan turunan dari fungsi logaritma.
Karena f(x) = ln (x), f-1(x) = ex
Dengan demikian, fungsi invers ln (x) adalah ex.
Jika f(x) = ln (x), maka x sama dengan ey.
Bagaimana ln (x) adalah turunan? Dijelaskan dalam submateri Turunan Fungsi Logaritma bahwa turunan dari ln (x) bernilai kebalikan dari x karena f(x) = ln (x) dan f'(x) =1/x.
Output dari ex adalah ex. [f(x) = ex, maka f'(x) = ex]
Bagaimana Turunan Invers Logaritma Bekerja? Konsep rumus turunan invers fungsi dapat digunakan untuk menghitung turunan dari fungsi invers logaritma natural, yang diwakili sebagai d/dx(ln-1 (x)) atau (ln-1 )'(x), jika f(x) = ex. Dengan asumsi bahwa (f-1)'(x) = g'(x), dan nilai g'(x) = (ln-1)'(x), maka persamaan dari (ln-1)'(x) diperoleh berdasarkan rumus bahwa (ln-1)'(x) = 1/ln'(ex), dan nilai g(x) = ex. Kemudian nilai ln'(ex) dapat diganti dengan 1/ex, sehingga diperoleh
Ex = (ln-1)'(x) = 1/(1/(ex))
Oleh karena itu, turunan invers logaritma natural adalah (ln-1)'(x) =ex, yang menunjukkan bahwa perubahan variabel x terhadap fungsi invers logaritma natural berhubungan dengan nilai fungsi itu sendiri.






Tidak ada komentar:
Posting Komentar