APLIKASI TURUNAN

Turunan adalah salah satu dasar analisis dan bisa digunakan untuk memecahkan permasalahan sehari-hari. Banyak sekali pekerjaan yang menggunakan aplikasi soal turunan.  Misalnya, perancangan bangunan atau menghitung kecepatan, kamu juga bisa menggunakan aplikasi turunan dalam kehidupan sehari-hari.

1. Kecepatan Rata-Rata, Kecepatan Sesaat dan Percepatan

    jika kita mengendarai mobil dari sebuah kota ke kota lain yang berjarak 80 km selama 2 jam, maka kecepatan rata-rata kita adalah 40km tiap jam. Kecepatan rata-rata adalah jarak dari posisi pertama ke posisi kedua dibagi dengan waktu tempuh. Ternyata turunan juga digunakan dalam rumus Fisika yang sering kita jumpai, yaitu kecepatan dan percepatan. Jika diketahui sebuah benda bergerak menempuh jarak s = f(t), maka kecepatan dan percepatan benda tersebut dapat dirumuskan sebagai berikut:

Kecepatan benda saat t detik (turunan pertama). Rumus turunan pertama yaitu

a. v = s' = ds/dt 

dimana s adalah jarak dan t adalah waktu

b. Percepatan benda saat t detik (turunan kedua). Rumusnya ialah:

v = s'' = d2s/dt2

2. Laju Perubahan

Kecepatan adalah suatu dari sekian banyak laju perubahan yang sangat penting dalam kuliah ini.  kecepatan adalah melaju perubahan jarak terhadap waktu. laju perubahan lain yang penting bagi kita adalah kepadatan (atau densitas) suatu kawat (laju perubahan massa terhadap jarak), pendapatan marjinal (laju perubahan pendapatan terhadap jenis produk), dan arus listrik (laju perubahan muatan listrik terhadap waktu). Dalam masing-masing kasus kita harus membedakan antara laju perubahan rata-rata pada suatu interval dan laju perubahan sesaat pada suatu titik. istilah laju perubahan tanpa keterangan apa-apa akan bermakna laju perubahan sesaat. 

a. Laju Perubahan Rata-Rata = Perbandingan antara perubahan jarak terhadap perubahan waktu 

Rumus : v rata-rata = Δs/Δt = f(t2) - f(t1)/ t2-t1

2. Laju Perubahan Sesaat

Rumus : v sesaat pada t1 = Limh → 0 f(t1 + h) - f(t1)/h

3. Gradien Persamaan Garis Singgung

Salah satu cara untuk membuat sebuah persamaan garis singgung adalah dengan menggunakan gradien atau kemiringan dari garis tersebut. Gradien suatu fungsi f(x) yang melalui titik A (a,f(a)) dapat ditentukan dengan menggunakan turunan dengan rumus: m = f’(a).

4. Masalah Benda Jatuh

Jika sebuah benda dilempar ke atas (atau ke bawah) dari suatu ketinggian awal s0 desimeter dengan kecepatan awal v0 desimeter/detik dan jika s adalah tingginya di atas tanah dalam desimeter setelah t detik, maka:

s = -16t + v0t + s0

ini mengasumsikan bahwa percobaan berlangsung dekat permukaan laut dan bahwa tekanan udara dapat diabaikan.

TURUNAN INVERS FUNGSI, TRIGONOMETRI, DAN LOGARITMA

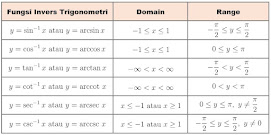
Turunan Invers Fungsi 

Dalam kalkulus, istilah "turunan invers fungsi" mengacu pada penghitungan turunan dari fungsi invers. Jika suatu fungsi f didefinisikan pada suatu interval dan memiliki fungsi invers f-1, turunan invers fungsi diwakili dengan f′-1 (x) atau (f-1)′(x).Oleh karena itu, jika fungsi f(x) adalah fungsi satu-satu kontinu atau fungsi bijektif yang didefinisikan pada suatu interval, katakanlah I, maka fungsi f(x) juga kontinu, dan jika fungsi f(x) adalah fungsi terdiferensiasi, maka fungsi f(x) juga terdiferensiasi. 

Rumus untuk Turunan Invers Fungsi adalah sebagai berikut:

Menurut rumus ini, untuk menghitung turunan invers suatu fungsi pada nilai tertentu, kita perlu mengetahui turunan fungsi awal pada nilai invers tersebut. 

Ini adalah prosedur umum untuk menghitung turunan invers fungsi:

a. Mengidentifikasi Fungsi Asli:

Misal, y = f(x) dan g(x) adalah fungsi f(x) yang berlawanan.

b. Perhitungan Turunan Fungsi Asli:

Cari turunan f'(x)

c. Untuk mengetahui nilai invers:

Cari nilai invers f-1(x) yang sesuai.

d. Hitung hasil invers:

Untuk menghitung (f-1)′(x), gunakan rumus sesuai langkah sebelumnya, alih-alih menggunakan f-1 (x) dan f'(f-1 (x).

Dalam situasi di mana kita memiliki informasi tentang perubahan suatu variabel terhadap variabel lainnya dan ingin mengetahui perubahan yang terkait dengan inversnya, penurunan invers fungsi sering digunakan.

Contoh soal:

cari turunan invers f(x) = 2x + 3.

Penyelesaian:

Misal f(x) = 2x + 3 dan g(x) adalah invers f(x), yaitu f-1(x). Untuk menghitung turunan invers g'(x), kita perlu mengetahui bahwa f'(x) = 2. Kemudian kita menggunakan rumus ini.

g'(x) = 1/f'(g(x)) = 1/2

Oleh karena itu, turunan fungsi g(x) terhadap x adalah 1/2.

Turunan Invers Trigonometri

Fungsi invers trigonometri menyebabkan penurunan trigonometri. Dalam trigonometri invers, kita memiliki enam fungsi yang merupakan kebalikan dari enam fungsi trigonometri dasar. Turunan trigonometri invers hanya dapat digambarkan dalam domain fungsi trigonometri invers, yang dapat dilihat sebagai berikut:

Turunan dari fungsi trigonometri invers adalah turunan dari fungsi trigonometri invers, seperti arcsin (atau sin-1), arccos (atau cos-1), dan arctan (atau tan-1), dll. Kami menemukan turunan dari fungsi trigonometri invers dengan menggunakan diferensiasi implisit, yang akan kami bahas secara rinci di bagian mendatang. Turunan invers trigonometri adalah sebagai berikut:

1. Tingkat penurunan arcsin x adalah d/dx(arcsin x) = 1/√1-x2, karena -1 < x < 1.

2. Jika -1 < x < 1, turunan arccos x adalah d/dx(arccos x) = -1/√1-x2.

3. Untuk semua x di R, turunan arctan x adalah d/dx(arctan x) = 1/(1+x2).

4. Ketika x < -1 atau x > 1, penurunan arccsc x adalah d/dx(arccsc x) = -1/(|x|√x2-1).

5. Ketika x < -1 atau x > 1, turunan arcsec x adalah d/dx(arcsec x) = 1/(|x|√x2-1).

6. Untuk semua x di R, turunan arccot x adalah d/dx(arccot x) = -1/(1+x2).

Turunan Invers Logaritma

Dengan mengikuti aturan dasar kalkulus, turunan dari fungsi invers logaritma natural (ln)—juga dikenal sebagai fungsi logaritma natural invers atau ln-1 (x), dan biasanya disebut sebagai exp(x) atau ex—melibatkan turunan dari fungsi logaritma.

Karena f(x) = ln (x), f-1(x) = ex 

Dengan demikian, fungsi invers ln (x) adalah ex.

Jika f(x) = ln (x), maka x sama dengan ey.

Bagaimana ln (x) adalah turunan? Dijelaskan dalam submateri Turunan Fungsi Logaritma bahwa turunan dari ln (x) bernilai kebalikan dari x karena f(x) = ln (x) dan f'(x) =1/x.

Output dari ex adalah ex. [f(x) = ex, maka f'(x) = ex]

Bagaimana Turunan Invers Logaritma Bekerja? Konsep rumus turunan invers fungsi dapat digunakan untuk menghitung turunan dari fungsi invers logaritma natural, yang diwakili sebagai d/dx(ln-1 (x)) atau (ln-1 )'(x), jika f(x) = ex.  Dengan asumsi bahwa (f-1)'(x) = g'(x), dan nilai g'(x) = (ln-1)'(x), maka persamaan dari (ln-1)'(x) diperoleh berdasarkan rumus bahwa (ln-1)'(x) = 1/ln'(ex), dan nilai g(x) = ex. Kemudian nilai ln'(ex) dapat diganti dengan 1/ex, sehingga diperoleh

Ex = (ln-1)'(x) = 1/(1/(ex))

Oleh karena itu, turunan invers logaritma natural adalah (ln-1)'(x) =ex, yang menunjukkan bahwa perubahan variabel x terhadap fungsi invers logaritma natural berhubungan dengan nilai fungsi itu sendiri.

KECEKUNGAN DAN SKETSA GRAFIK

Teori Kecekungan

Lihat gambar di bawah ini. Kita dapat mengatakan bahwa f naik di kanan c dan turun di kiri c. Definisi presisinya adalah sebagai berikut.

Misalkan f didefinisikan pada interval I (buka, tutup, atau buka keduanya). 

1. Untuk setiap pasangan bilangan x1 dan x2 dalam I, dikatakan bahwa f naik pada I jika x1 < x2 → f(x1) < f(x2). 

2. Jika untuk setiap pasangan bilangan x1 dan x2 dalam I x1 < x2 → f(x1) > f(x2) maka f turun pada I. 

3. Jika f meningkat atau menurun pada I, f monoton murni pada I. 

A. Keturunan Pertama dan Kemonotan

Ingatlah bahwa turunan pertama f'(x) memberikan kemiringan dari garis singgung pada grafik f di titik x. Oleh karena itu, jika f'(x) > 0, maka garis singgung menaik ke kanan, yang menunjukkan bahwa f menaik, dan jika f'(x) < 0, maka garis singgung menurun ke kanan, menunjukkan bahwa f menurun. 

Ini adalah teorema kemotonan.

Dalam contoh berikut, fungsi f dapat didiferensialkan pada titik dalam selang I. Jika f′ (x) lebih besar dari 0 untuk semua titik dalam x dari I, maka f naik pada I, dan jika f′ (x) kurang dari 0 untuk semua titik dalam x dari I, maka f turun pada I. Teorema ini memungkinkan kita untuk mengetahui dengan tepat di mana suatu fungsi yang didiferensiasi naik dan di mana fungsi tersebut turun. Ini adalah tugas menyelesaikan dua ketidaksamaan.

Contoh soal:

Jika f(x) = 2x3 - 3x2 - 12x + 7, cari dimana f naik dan di mana f turun.

Penyelesaian:

Kita mulai dengan mencari turunan f 

f' (x) = 6x2 - 6x - 12 = 6(x +1)(x-2)

Kita perlu menentukan nilai x yang memenuhi

(x + 1)(x - 2) > 0

dan juga memenuhi 

(x + 1)(x - 2) < 0

Titik-titik pemisah adalah -1 dan 2, yang membagi sumbu-x atas tiga interval (-∞  ,-1), (-1, 2) dan (2, ∞ ). Dengan menggunakan titik-titik uji -2,0, dan 3, kita simpulkan bahwa f'(x) > 0 pada interval pertama dan terakhir dan terakhir dan bahwa f'(x) < 0 pada interval tengah (Gambar 1).

Jadi menurut Teorema A, f naik pada (-∞, -1) dan (2, ∞); turun pada (-1, 2). Grafik f diperlihatkan dalam Gambar 2

B. Turunan dan Kecekungan Kedua

Mungkin ada fungsi yang menarik yang tetap memiliki grafik yang sangat bergerak. Untuk menganalisis goyangan, kita harus memahami bagaimana garis singgung bergerak dari kiri ke kanan pada grafik. Jika garis singgung bergerak secara tetap dalam arah yang berlawanan dengan putaran jarum jam, maka grafik cekung ke atas. Jika garis singgung bergerak searah dengan putaran jarum jam, maka grafik cekung ke bawah. Ini adalah definisi yang lengkap.

Misalnya, f dapat didiferensialkan pada selang terbuka I. 

1. Jika f ′ naik pada I, itu berarti f cekung ke atas naik pada I. 

2. jika f ′ turun pada I, itu berarti f cekung ke bawah naik pada I. 

Teorema Kecekungan dapat ditemukan di sini.

Misalnya, f dapat didiferensialkan dua kali pada titik dalam selang I

1. jika f ′′(x) > 0 untuk semua titik dalam x dari I, maka f cekung ke atas pada I, 

2. jika f ′′(x) < 0 untuk semua titik dalam x dari I, maka f cekung ke bawah pada I.

Teorema ini mengubah masalah penentuan kecekungan menjadi masalah menyelesaikan pertidaksamaan untuk sebagian besar fungsi.

Teori Sketsa Grafik

Kalkulus menyediakan alat ampuh untuk menganaliis struktur grafik secara baik, khususnya dalam mengenali titik-titik tempat terjadinya perubahan ciri-ciri grafik. Kita dapat melokasikan titik-titik maksimum lokal, titik-titik minimum lokal, dan titik-titik belok; kita dapat menentukan secara persis tempat grafik menaik atau tempat cekung ke atas. 

Dalam menggambarkan grafik fungsi, tidak terdapat pengganti untuk akal sehat. Tetapi, dalam banyak hal prosedur berikut akan sangat membantu.

Langkah 1 : Analisis Prakalkulus

1. Periksa daerah asal dan daerah hasil fungsi untuk melihat apakah ada daerah di bidang yang dikecualikan.

2. Uji kesimetrian terhadap sumbu-y dan titik asal. (Apakah fungsi genap atau ganji).

3. Cari perpotongan dengan sumbu-sumbu koordinat.

Langkah 2 : Analisis Kalkulus

1. Gunakan turunan pertama untuk mencari titik-titik kritis dan mengetahui tempat-tempat grafik menaik dan menurun

2. Uji titik-titik kritis untuk maksimum dan minimum lokal.

3. Gunakan turunan kedua untuk mengetahui tempat-tempat grafik cekung ke atas dan cekung ke bawah dan untuk melokasikan titik balik.

4. Cari asimtot-asimtot

Langkah 3 : Gambarkan beberapa titik (termasuk semua titik kritis dan titik belok).

Langkah 4 : Sketsakan Grafik.

NILAI EKSTRIM FUNGSI DAN TEOREMA NILAI RATA-RATA

Nilai Ekstrim Fungsi

A. Maksimum dan Minimum

     Misalkan, seperti yang ditunjukkan dalam Gambar berikut, kita diberikan fungsi f(x) dan daerah asal S. Sekarang kita memiliki tiga pertanyaan: Apakah f(x) memiliki nilai maksimum atau minumum pada S? Jika f(x) memiliki nilai maksimum atau minimum, di manakah nilai-nilai tersebut dicapai? Berapakah nilai maksimum dan minimum yang mungkin ada jika ada nilai-nilai tersebut? Lihatlah definisi berikut untuk menentukan jawaban atas pertanyaan Anda.

Misalkan 𝑆 adalah daerah asal 𝑓, mengandung titik 𝑐, kita katakan bahwa: 

1. jika 𝑓(𝑐) ≥ f(x) untuk semua x di 𝑆, maka 𝑓(𝑐) adalah nilai maksimum 𝑆

2. jika 𝑓(𝑐) ≤ f(x) untuk semua x di S, maka 𝑓(𝑐) adalah nilai minimum S

3. 𝑓(𝑐) adalah nilai ekstrim 𝑓 pada 𝑆 jika ia adalah nilai maksimum atau nilai minimum

4. Fungsi objektif adalah fungsi yang ingin kita maksimumkan atau minimumkan.

Sebuah teorema baik menentukan keberadaan nilai maksimum dan minimum: "Jika f kontinu pada interval tertutup [a, b], maka f mencapai nilai maksimum dan nilai minimum di sana." F harus kontinu, dan himpunan S harus tertutup interval.

B. Letak Terjadinya Nilai Ekstrim

     Fungsi objektif biasanya memiliki interval I sebagai daerah awalnya. Dalam teorema titik kritis berikut, sebarang titik dalam daerah asal fungsi f yang termasuk salah satu dari tiga kategori titik berikut akan dianggap sebagai titik kritis.

Misalkan f didefinisikan pada interval I yang memuat c; jika f(c) adalah nilai ekstrim, maka c haruslah titik kritis, yaitu: 

1. Titik ujung dari I 

2. Titik stationer dari 𝑓, yakni 𝑓 ′ (𝑐) = 0 

3. Titik singular dari 𝑓, yakni 𝑓′(𝑐) tidak ada 

Metode untuk menemukan nilai fungsi maksimum dan minimum di selang tutup:

1. Cari titik-titik kritis dari 𝑓 pada selang tutup yang diberikan. 

2. Cari nilai 𝑓 pada titik-titik kritis. 

3. Nilai yang paling besar pada langkah ke-2 menjadi nilai maksimum dan yang paling kecil menjadi nilai minimum. 

C. Ekstrim Lokal

Berikut ini definisi formal dari maksimum lokal dan minimum lokal.
Misal 𝑆 adalah daerah asal 𝑓 dan 𝑐 𝜖 𝑆. Dapat dikatakan bahwa : 
1. 𝑓(𝑐) nilai maksimum lokal 𝑓 pada 𝑆 jika terdapat selang buka I yang memuat 𝑐 sedemikian sehingga 𝑓(𝑐) ≥ 𝑓(𝑥),∀𝑥 ∈ Ι ⋂ 𝑆 
2. 𝑓(𝑐) nilai maksimum lokal 𝑓 pada 𝑆 jika terdapat selang buka I yang memuat 𝑐 sedemikian sehingga 𝑓(𝑐) ≤ 𝑓(𝑥),∀𝑥 ∈ Ι ⋂ 𝑆 
3. 𝑓(𝑐) nilai ekstrim lokal 𝑓 pada 𝑆 jika 𝑓(𝑐) nilai maksimum lokal atau nilai minimum lokal 

Dimana Nilai-Nilai Ektrim Lokal Terjadi? Berikut dipaparkan Teorema Uji pertama dan Uji kedua Ektrim Lokal
a. Teorema Uji Pertama Ekstrim Lokal 
Misal 𝑓 dapat didiferensialkan pada selang buka (a,b)yang memuat titik kritis 𝑐. 
1. Jika 𝑓 ′ (𝑥) > 0 untuk semua 𝑥 ∈ (𝑎, 𝑐) dan 𝑓 ′ (𝑥) < 0 untuk semua titik 𝑥 ∈ (𝑎, 𝑐), maka 𝑓(𝑐) adalah nilai maksimum local. 
2. Jika 𝑓 ′ (𝑥) < 0 untuk semua 𝑥 ∈ (𝑎, 𝑐) dan 𝑓 ′ (𝑥) > 0 untuk semua titik 𝑥 ∈ (𝑎, 𝑐), maka 𝑓(𝑐) adalah nilai maksimum lokal. 
3. Jika 𝑓 ′ (𝑥) bertanda sama untuk kedua belah pihak c, maka f (c) bukan nilai ekstrim f 

b. Teorema Uji Kedua Ekstrim Lokal 

Misal 𝑓 dan 𝑓 ′ dapat didiferensialkan pada selang buka (a,b) yang memuat titik 𝑐 dengan 𝑓 ′ (𝑐) = 0 

1. Jika 𝑓(𝑐) > 0 maka 𝑓(𝑐) adalah nilai minimum lokal. 

2. Jika 𝑓(𝑐) < 0 maka 𝑓(𝑐) adalah nilai maksimum lokal. 

TEOREMA NILAI RATA-RATA

Dalam bahasa geometri, Teorema Nilai Rataan mudah dinyatakan dan dipahami. Teorema mengatakan bahwa jika grafik sebuah fungsi kontinu mempunyai garis singgung tak tegak pada setiap titik antara A dan B, maka terdapat paling sedikit satu titik C pada grafik di antara A dan B sehingga garis singgung di titik C sejajar tali-busur AB. Gambar 1 hanya terdapat 1 titik C dan Gambar 2 terdapat beberapa titik C.

Teorema Nilai Rataan untuk Turunan

1. Jika f kontinu pada interval tertutup [a,b] dan terdiferensiasikan pada titik dalamnya (a,b) maka terdapat paling sedikit satu biangan c dalam (a,b) di mana

f(b) - f(a)/b - a = f'(c)

Atau, secara setara,

f(b) - f(a) = f'(c) (b-a)

2. Jika F'(x) = G'(x) untuk semua x dalam (a,b) maka terdapat konstanta C sedemikian rupa sehingga F(x)=G(x) + C untuk semua x dalam (a,b).

Contoh Soal

Carilah bilangan c yang dijamin oleh Teorema Nilai Rataan untuk f(x) - 2√x pada [1,4]
Penyelesaian
f'(x) = 2 . (1/2x)-1/2 = 1/√x
dan
f(4) - f(1)/4 -1 = 4 -2/3 = 2/3
Jadi kita harus menyelesaikan 
1/√c = 2/3
Penyelesaian tunggalnya adalah c = 9/4 (ditunjukkan pada gambar)

TURUNAN TINGKAT TINGGI DAN TURUNAN IMPLISIF

Turunan Tingkat Tinggi

Operasi diferensiasi mengambil sebuah fungsi f dan menghasilkan fungsi baru f. Jika kita mendiferensiasikan f', kita akan menghasilkan fungsi lain, yang disebut f" (baca "f bilangan prima ganda") dan disebut turunan kedua. Selanjutnya, fungsi tersebut dapat didiferensiasikan untuk menghasilkan f"', yang disebut turunan ketiga. Turunan keempat diwakili dengan f^(4), turunan kelima diwakili dengan f^(5), dan seterusnya

Sebagai contoh:

f(x) = 2x3 - 4x2 + 7x - 8

maka :

f'(x) = 6x2 + 8x + 7

f''(x) = 12x + 8

f'''(x) = 12

f4 (x) = 0

Turunan keempat dan semua turunan orde tinggi dari f adalah nol karena turunan dari fungsi nol adalah nol.

Turunan (sekarang disebut sebagai turunan pertama) dari y = f(x) telah diperkenalkan dengan tiga notasi, yaitu

Mereka disebut notasi prima, notasi D, dan notasi Leibniz, masing-masing. Ada juga varian notasi prima, y, yang kita akan gunakan sedikit. Tabel terlampir menunjukkan bahwa semua notasi ini memiliki ekstensi untuk turunan tingkat tinggi. Penting untuk memperhatikan notasi Leibniz, yang, meskipun rumit, tampaknya paling cocok untuk Leibniz. Dia berpendapat bahwa tidak ada yang lebih alami daripada menulis.

contoh soal:

Turunan Implisit

Dalam persamaan 

y3 + 7y = x3, 

kita tidak dapat memecahkan y dalam bentuk x, tetapi mungkin tetap ada kasus bahwa terdapat tepat satu y yang berhubungan dengan masing-masing x. Misalnya, kita dapat menanyakan berapa nilai-nilai y yang berhubungan dengan x = 2, dan untuk menjawab pertanyaan ini, kita harus memecahkan persamaan 

y3 + 7y = 8. 

Tentu saja, y = 1 adalah satu penyelesaian, dan ternyata y Kita katakan bahwa persamaan mendefinisikan y sebagai fungsi implisit. Gambar 1 menunjukkan grafik persamaan ini, yang jelas terlihat seperti grafik suatu fungsi yang berbeda. Elemen baru ini tidak berbentuk y=f(x). Berdasarkan grafik, kita menganggap bahwa y adalah fungsi yang tidak diketahui dari. Jika kita menunjukkan fungsi ini oleh y(x), kita dapat menulis persamaan tersebut sebagai

y(x) tidak memiliki rumus, tetapi kita dapat memperoleh hubungan antara y(x), dan y(x) dengan mendiferensiasikan kedua ruas persamaan itu terhadap x. Dengan menggunakan Aturan rantai kita memperoleh 

contoh soal:

TURUNAN FUNGSI TRIGONOMETRI, EKSPONENSIAL DAN LOGARITMA

Turunan Fungsi Trigonometri

Salah satu cabang matematika adalah trigonometri, yang berkaitan dengan sudut segitiga dan fungsi trigonometri seperti sin, cos, dan tan. Sementara turunan adalah laju perubahan suatu fungsi terhadap perubahan peubahnya. Untuk situasi di mana tingkat perubahan fungsi terletak pada titik a, turunan f(x) ditulis sebagai f'(a). Oleh karena itu, turunan trigonometri adalah proses matematis untuk mendapatkan turunan dari sebuah fungsi trigonometri. Sementara itu, suatu fungsi baru dapat disebut f' (dibaca dengan aksen f). Sin x, cos x, dan tan x adalah fungsi trigonometri umum.

Semua fungsi trigonometri memiliki karakteristiknya sendiri. Perbedaannya tergantung pada jenis bangun segitiga dan besar sudut masing-masing. Sebelum Anda dapat memahami turunannya, Anda harus terlebih dahulu memahami setidaknya tiga fungsi trigonometri yang sering muncul. Ini adalah penjelasannya:

1. sinus (Sin)

Ketika sudut segitiga siku-siku atau salah satu sudutnya 90 derajat, fungsi trigonometri sinus digunakan untuk membandingkan sisi depan segitiga dengan sisi miringnya. Di kuadrannya, fungsi sinus memiliki nilai yang positif dan negatif. Kuadran I dan II menunjukkan sinus positif, sementara kuadran III dan IV menunjukkan sinus negatif.

2. Cosinus (Cos) 

Fungsi trigonometri cosinus ini adalah perbandingan sisi segitiga yang terletak di sudut dengan sisi miring. Perbandingan ini digunakan dengan catatan segitiga itu adalah segitiga siku-siku atau salah satu sudutnya sebesar 90 derajat. Fungsi cosinus turut memiliki nilai negatif dan positif. Nilai positifnya berada di kuadran I dan IV, sementara nilai negatifnya ada di kuadran II dan III.

3. Tangen (Tan)

Fungsi trigonometri tangen ini berupa perbandingan sisi segitiga yang terletak di depan sudut, dengan sisi segitiga di bagian sudut segitiga tersebut. Perbandingan ini digunakan jika segitiga berupa siku-siku atau salah satu sudutnya sebesar 90 derajat. Fungsi ini memiliki nilai negatif dan positif seperti fungsi trigonometri lainnya. Nilai positifnya berada di kuadran I dan III, nilai negatifnya ada di kuadran II dan IV.

Rumus Turunan Fungsi Trigonometri 

Adapun rumus turunan fungsi trigonometri yang memuat fungsi trigonometri berupa sin, cos, tan, cot, sec, dan csc. Berikut ini rumus-rumus tersebut: 

1. Jika f (x) = sin x, maka artinya f '(x) = cos x 

2. Jika f (x) = cos x, maka artinya f '(x) = −sin x 

3. Jika f (x) = tan x, maka artinya f '(x) = sec2 x 

4. Jika f (x) = cot x, maka artinya f '(x) = −csc2x 

5. Jika f (x) = sec x, maka artinya f '(x) = sec x . tan x 

6. Jika f (x) = csc x, maka artinya f '(x) = −csc x . cot x

contoh soal:

1. Tentukan y’ dari y = -2 cos x 

Jawaban: 

y = -2 cos x 

y’ = -2 (-sin x)

sehingga, y’ = 2 sin x

2. Tentukan hasil dari f (x) = sin (2x + 10) 

Jawaban: 

f(x) = sin (2x + 10)  

f’(x) = 2 cos (2x + 10) 

sehingga, y' = 2 cos (2x + 10) 

3. Tentukan y’ dari y = 4 sin x + 5 cos x 

Jawaban: 

y = 4 sin x + 5 cos x 

y’ = 4 (cos x) + 5 (-sin x) 

sehingga, y’ = 4 cos x – 5 sin x

Turunan Fungsi Eksponensial

Sebelum membahas lebih jauh tentang turunan fungsi eksponensial, Anda harus mempelajari materi prasyaratnya terlebih dahulu. Turunan fungsi eksponensial agak berbeda dari turunan fungsi aljabar dan turunan fungsi trigonometri.

Mencari bilangan e untuk penurunan fungsi eksponensial

Nilai bilangan real positif e = 2,718281828459, dan rumusnya adalah:

Rumus-rumus turunan fungsi eksponensial

Contoh soal:

Tentukan turunan dari fungsi-fungsi dibawah ini!

(1). Tentukan turunan dari :

 

[penyelesaian]

2). Tentukan turunan dari :

 

[penyelesaian]

Turunan Fungsi Logaritma

Fungsi yang merupakan kebalikan dari fungsi eksponensial disebut fungsi logaritma. Direpresentasikan sebagai log b x, dimana b adalah alas log. Nilai x adalah nilai yang sama dengan basis logaritma yang dipangkatkan ke bilangan tetap y, sehingga bentuk umum fungsi logaritma adalah:

y = log bx

Di mana,

• y adalah logaritma dari x,
• b adalah basis logaritma, dan 
• x adalah input logaritma.

Beberapa properti fungsi logaritma tercantum di bawah ini:

• log (XY) = log X + log Y
• log (X / Y) = log X – log Y
• catatan X Y = Y catatan X
• log Y X = ln X / ln Y

Rumus turunan fungsi logaritma yang tersedia adalah sebagai berikut.

Turunan dari ln x, log an x, dan ln f(x)

Mari kita bahas rumus ini.

Turunan ln x: Turunan ln x bernilai kebalikan dari x, dengan rumus berikut: (d / dx) dalam x = 1 / x, di mana x lebih besar dari 0.

Turunan log an x: Turunan log dengan basis a dan nilai x bernilai kebalikan dari hasil kali x dan ln a. Rumus turunan log an x adalah: (d/dx) log an x = 1 / [x ln a] Dimana, a ≠ 1.

Turunan ln f(x) : Turunan ln f(x) dapat dihitung sebagai turunan dari f(x) dibagi f(x). Rumus turunan ln f(x) adalah: (d/dx) dalam f(x) = f'(x) / f(x), di mana f(x) adalah sembarang fungsi dari x, dan f'(x) adalah turunan dari fungsi x.

Contoh soal:

(i) Turunan dari log 2x
(ii) Turunan dari log 10 x
(iii) Turunan dari log y
jawaban:

(i) Turunan dari log2x
⇒ (d / dx) [log 2x] = (d / dx) [log 2x](d / dx) [2x]
⇒ (d / dx) [log 2x] = 2 / (2x)
⇒ (d/dx) [log 2x] = 1/x
(ii) Turunan dari log 10 x
⇒ (d / dx) [log 10 x] = 1 / [x ln 10]
(iii) Turunan dari log y
⇒ (d / dx) [log y] = [1 / y](dy / dx)